«а2». оборудование для автосервиса

Квадрат суммы

Пусть у нас возводиться в квадрат сумма двух одночленов, вот так: \((a+b)^2\). Возведение в квадрат – это умножение числа или выражения само на себя, то есть, \((a+b)^2=(a+b)(a+b)\). Теперь мы можем просто раскрыть скобки, перемножив их как делали это здесь, и привести подобные слагаемые. Получаем:

А если мы опустим промежуточные вычисления и запишем только начальное и конечное выражения, получим окончательную формулу:

Квадрат суммы: \((a+b)^2=a^2+2ab+b^2\)

Большинство учеников учат ее наизусть. А вы теперь знаете, как эту формулу вывести, и если вдруг забудете – всегда можете это сделать.
Хорошо, но как ей пользоваться и зачем эта формула нужна? Квадрат суммы позволяет быстро писать результат возведения суммы двух слагаемых в квадрат. Давайте посмотрим на примере.

Пример. Раскрыть скобки: \((x+5)^2\)Решение:

Обратите внимание, насколько быстрее и меньшими усилиями получен результат во втором случае. А когда вы эту и другие формулы освоите до автоматизма – будет еще быстрее: вы сможете просто сразу же писать ответ

Поэтому они и называются формулы СОКРАЩЕННОГО умножения. Так что, знать их и научиться применять – точно стоит.

На всякий случай отметим, что в качестве \(a\) и \(b\) могут быть любые выражения – принцип остается тем же. Например:

Если вы вдруг не поняли какие-то преобразования в двух последних примерах – повторите свойства степеней и тему приведения одночлена к стандартному виду.

Пример. Преобразуйте выражение \((1+5x)^2-12x-1 \) в многочлен стандартного вида.

Решение:

\((1+5x)^2-12x-1= \)		Раскроем скобки, воспользовавшись формулой квадрата суммы…
\(=1+10x+25x^2-12x-1=\)		…и приведем подобные слагаемые.
\(=25x^2-2x\)		Готово.

Ответ: \(25x^2-2x\).

Важно! Необходимо научиться пользоваться формулами не только в «прямом», но и в «обратном» направлении.

Пример. Вычислите значение выражения \((368)^2+2·368·132+(132)^2\) без калькулятора.

Решение:

\((368)^2+2·368·132+(132)^2=\)

               

Мда… возводить в квадрат трехзначные числа, перемножить их же, а потом все это складывать – удовольствие ниже среднего

Давайте искать другой путь: обратите внимание, что данное нам числовое выражение очень похоже на правую часть формулы. Применим ее в обратную сторону: \(a^2+2ab+b^2=(a+b)^2\)

\(=(368+132)^2=\)

 

Вот теперь вычислять гораздо приятнее!

\(=(500)^2=250 000.\)

 

Готово.

Ответ: \(250 000\).

Для США

рестайлинг, 2 поколение, 06.2004 — 06.2008, Хэтчбек 5 дв.

Комплектация	Период выпуска	Цена	Марка двигателя	Марка кузова
2.0 л, 200 л.с., Бензин, МКПП, Передний (FF)
2.0 TFSI MT	02.2005 — 09.2008		AXX, BPY, BWA, CAWB, CCZA	8PA
2.0 л, 200 л.с., Бензин, Робот, Передний (FF)
2.0 TFSI S tronic	02.2005 — 09.2008		AXX, BPY, BWA, CAWB, CCZA	8PA
3.2 л, 250 л.с., Бензин, Робот, Полный (4WD)
3.2 S tronic quattro S Line	02.2005 — 09.2008		BDB, BMJ, BUB	8PA

Б/У Двигатель Audi A3 седан III 2.0 TDI quattro CUNA

Б/У Двигатель Audi A3 кабрио III 2.0 TDI quattro CRLB

Б/У Двигатель Audi A3 Sportback II 2004 — 2013 1.6 TDI CAYC

Б/У Двигатель Audi A3 хэтчбек III 2.0 TDI quattro CUNA

Б/У Двигатель Audi A3 седан III 2.0 TDI CRBD, CRLC

Б/У Двигатель Audi A3 хэтчбек II 2.0 TDI BUY

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)2.

Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)

(2x + 3y)2 = (2x + 3y)(2x + 3y)

Получили умножение многочлена на многочлен. Выполним его:

(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4×2 + 6xy + 6xy + 9y2 = 4×2 + 12xy + 9y2

То есть выражение (2x + 3y)2 равно 4×2 + 12xy + 9y2

(2x + 3y)2 = 4×2 + 12xy + 9y2

Решим аналогичный пример, который попроще:

(a + b)2

Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (a + b)

(a + b)2 = (a + b)(a + b)

Выполним это умножение:

(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2

То есть выражение (a + b)2 равно a2 + 2ab + b2

(a + b)2 = a2 + 2ab + b2

Оказывается, что случай (a + b)2 можно распространить для любых a и b. Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y

a = 2x

b = 3y

И далее можно воспользоваться тождеством (a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:

(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4×2 + 12xy + 9y2

Как и в прошлый раз получили многочлен 4×2 + 12xy + 9y2. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:

(2x + 3y)2 = 4×2 + 12xy + 9y2

Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3)2 = 52 = 25

Второй способ:

(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25

Пример 2. Преобразовать выражение (5a + 3)2 в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9

Значит, (5a + 3)2 = 25a2 + 30a + 9.

Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:

(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9

Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.

Например, площадь квадрата со стороной a будет равна a2. Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b

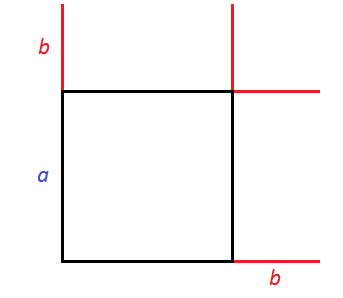
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:

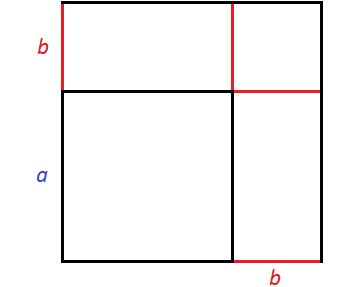
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.

Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b

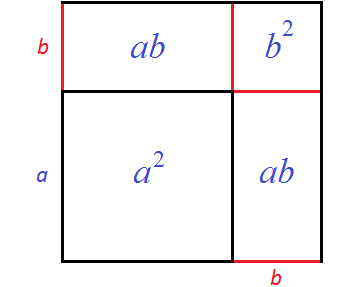
В результате получается следующая сумма площадей:

a2 + ab + ab + b2

Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Выводим формулу корней квадратного уравнения

Продолжим изучать формулу корней квадратного уравнения.

Пусть перед нами есть задача решить квадратное уравнение ax2 + bx + c = 0. Выполним ряд равносильных преобразований:

• разделим обе части этого уравнения на отличное от нуля число a, после чего получим приведенное квадратное уравнение:
• выделим полный квадрат левой части нового уравнения:

  ,

  после чего уравнение примет вид

• перенесем два последних слагаемых в правую часть и сменим знак на противоположный:
• преобразуем выражение в правой части:

Так, мы пришли к уравнению , которое полностью равносильно исходному ax2 + bx + c = 0.

Отсюда выводы про корни уравнения :

И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части

При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D

По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.

Повторим:

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения

Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b2−4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = — b2/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4×2 + 28x — 49 = 0.

Как решаем:

1. Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

   х = — 28/2(-4)

   х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6×2 = 0.

Как решаем:

1. Произведем равносильные преобразования. Умножим обе части на −1

   54 — 6×2 = 0 | *(-1)

   6×2 — 54 = 0

2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   6×2 = 54

   х2 = 9

   х = ±√9

   х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x2— х = 0.

Как решаем:

1. Преобразуем уравнение так, чтобы появились множители

   х(х — 1) = 0

   х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x2— 10 = 39.

Как решаем:

1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   x2— 10 = 39

   x2= 39 + 10

   x2= 49

   х = ±√49

   х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3×2— 4x+94 = 0.

Как решаем:

1. Найдем дискриминант по формуле

   D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112

2. Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Приходите решать примеры на бытовых ситуациях, с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный пробный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.

Технические характеристики

Процесс производства и все технические параметры арматуры класса А2 контролируются нормативными документами ГОСТ 10884-81 и ГОСТ 578-82. Она относится к металлопрокату, для которого характерны круглое сечение и рыхленная выпуклая поверхность. Именно благодаря такому типу поверхности обеспечивается максимальный уровень сцепки арматуры и бетона.

Арматура А300 обладает следующими техническими характеристиками:

• диаметр – от 10 мм до 80 мм;

• материал для изготовления – конструкционная сталь углеродистая обыкновенная.

После изготовления на поверхность арматуры в обязательном порядке наносится маркировка Ст5сп или Ст5пс. Первая аббревиатура означает, что для изготовления арматуры использовалась сталь спокойной степени раскисления, вторая – полуспокойного.

Изделие металлопроката класса А2 диаметром до 12 мм поступает в продажу в мотках, вся остальная – в виде отдельных металлических стержней.

Арматура А300 обладает отличными техническими параметрами, она:

• прочная;

• надежная;

• выдерживает высокие нагрузки;

• коррозиестойкая.

Металлопрокат А2 бывает:

• проволочным;

• канатным;

• напрягаемым;

• ненапрягаемым.

Каждый из вышеперечисленных видов арматуры предназначен для определенного использования и выдерживает определенные нагрузки.

Изделие металлопроката класса А2 изготавливается двумя способами – холоднокатаным и горячекатаным. Варианты производства влияет на сферу применения материала и его технические параметры. Более прочной считается арматура, которая изготовлена холоднокатаным способом. Такой материал способен выдержать колоссальные нагрузки, при этом вовсе не деформироваться.

Как узнать, что материал изготовлен холоднокатаным способом? Все очень просто: нужно взглянуть на поверхность изделия. Она более ровная, на ней нет перепадов.

Горячекатаное изделие на поверхности имеет перепады по диаметру. Это связано с тем, что сталь не прогревается одинаково, и при формировании прутьев в местах недогрева диаметр может быть другим. Именно поэтому такая арматура стоит значительно дешевле.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения 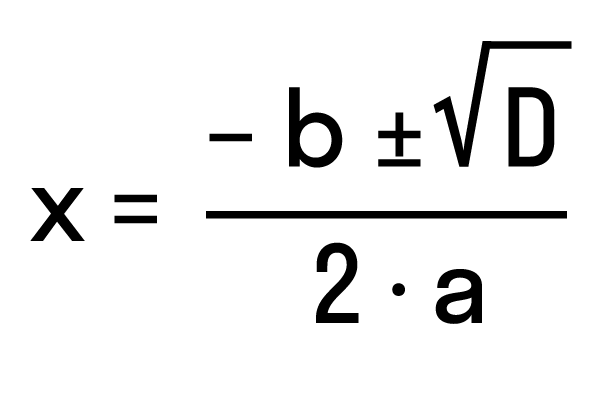, где D = b2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2- 4ac = 4n2 — 4ac = 4(n2- ac) и подставим в формулу корней:

Для удобства вычислений обозначим выражение n2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n2- ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n2- ac;
• если D₁< 0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле;
• если же D₁> 0, значит можно найти два действительных корня по формуле

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11×2 — 4 x — 6 = 0, чем 1100×2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100×2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12×2- 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2×2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2×2- 3x + 7 = 0 перейти к решению 2×2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

• x₁ + x₂ = — b/a,
• x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3×2- 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Разложение формул сокращенного умножения

Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.

Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:

a2 + b2 = (a + b)2 — 2ab.

Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)2 — 2ab = (a + b)(a + b) — 2ab = a2 + ab + ab + b2 — 2ab = a2 + b2.

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

a2 — b2 = (a + b)(a — b).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)(a — b) = a2 — ab + ab — b2 = a2 — b2.

Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

(a + b)2 = a2 + 2ab + b2.

Доказательство: представим степень в виде произведения, выполним умножение и :

(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2.

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:

(a — b)2 = a2 — 2ab + b2.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b)2 = (a — b)(a — b) = a2 — ab — ab + b2 = a2 — 2ab + b2.

Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:

a3 + b3 = (a + b)(a2 — ab + b2).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)(a2 — ab + b2) = a3 — a2b + ab2 + a2b — ab2 + b3 = a3 + b3.

Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:

a3 — b3 = (a — b)(a2 + ab + b2).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a — b)(a2 + ab + b2) = a3 + a2b + ab2 — a2b — ab2 — b3 = a3 — b3.

Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:

(a + b)3 = a3 + 3a2b + 3ab2 + b3.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b)3 = (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3.

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

(a — b)3 = a3 — 3a2b + 3ab2 — b3.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b)3 = (a — b)(a — b)2 = (a — b)(a2 — 2ab + b2) = a3 — 2a2b + ab2 — a2b + 2ab2 — b3 = a3 — 3a2b + 3ab2 — b3.

Разность квадратов

Итак, мы разобрались с ситуациями произведения двух скобок с плюсом в них и двух скобок с минусом. Остался случай произведения одинаковых скобок с разными знаками. Смотрим, что получится:

Получили формулу:

Разность квадратов \(a^2-b^2=(a+b)(a-b)\)

Эта формула одна из наиболее часто применяемых при разложении на множители и работе с алгебраическими дробями. 

Пример. Сократите дробь \(\frac{x^2-9}{x-3}\).

Решение:

\(\frac{x^2-9}{x-3}\)\(=\)		Да, я знаю, что рука так и тянется сократить иксы и девятку с тройкой – однако так делать ни в коем случае нельзя, ведь и в числителе, и в знаменателе стоит минус! Попробуем воспользоваться формулой.
\(=\) \(\frac{x^2-3^2}{x-3}\)\(=\)\(\frac{(x+3)(x-3)}{x-3}\)\(=\)		Вот теперь все плюсы и минусы попрятались в скобки, и значит без проблем можем сокращать одинаковые скобки.
\(=x+3\)		Готов ответ.

Ответ: \(x+3\).

Пример.Разложите на множители \(25x^4-m^{10} t^6\). Решение:

\(25x^4-m^{10} t^6\)		Воспользуемся формулами степеней: \((a^n )^m=a^{nm}\) и \(a^n b^n=(ab)^n\).
\(=(5x^2 )^2-(m^5 t^3 )^2=\)		Ну, а теперь пользуемся формулой \(a^2-b^2=(a+b)(a-b)\), где \(a=5x^2\) и \(b=m^5 t^3\).
\(=(5x^2-m^5 t^3 )(5x^2+m^5 t^3 )\)		Готов ответ.

Это три основные формулы, знать которые нужно обязательно! Есть еще формулы с кубами (см. выше), их тоже желательно помнить либо уметь быстро вывести. Отметим также, что в практике часто встречаются сразу несколько таких формул в одной задаче – это нормально. Просто приучайтесь замечать формулы и аккуратно применяйте их, и все будет хорошо.

Пример (повышенной сложности!).Сократите дробь \(\frac{x^2-4xy-9+4y^2}{x-2y+3}\) . Решение:

\(\frac{x^2-4xy-9+4y^2}{x-2y+3}\)\(=\)		На первый взгляд тут тихий ужас и сделать с ним ничего нельзя (вариант «лечь и помереть» всерьез не рассматриваем). Однако давайте попробуем поменять два последних слагаемых числителя местами и добавим скобки (просто для наглядности).
\(\frac{(x^2-4xy+4y^2)-9}{x-2y+3}\)\(=\)		Теперь немного преобразуем слагаемые в скобке: \(4xy\) запишем как \(2·x·2y\), а \(4y^2\) как \((2y)^2\).
\(\frac{(x^2-4xy+(2y)^2)-9}{x-2y+3}\)\(=\)		Теперь приглядимся – и заметим, что в скобке у нас получилась формула квадрата разности, у которой \(a=x\), \(b=2y\). Сворачиваем по ней к виду скобки в квадрате. И одновременно представляем девятку как \(3\) в квадрате.
\(\frac{(x-2y)^2-3^2}{x-2y+3}\)\(=\)		Еще раз внимательно смотрим на числитель… думаем… думаем… и замечаем формулу разности квадратов, у которой \(a=(x-2y)\), \(b=3\). Раскладываем по ней к произведению двух скобок.
\(\frac{(x-2y-3)(x-2y+3)}{x-2y+3}\)\(=\)		И вот теперь сокращаем вторую скобку числителя и весь знаменатель.
\(x-2y-3\)		Готов ответ.

Задания для самостоятельного решения

Задание 1. Преобразуйте выражение (m + n)2 в многочлен.

Решение:
(m + n)2 = m2 + 2mn + n2

Задание 2. Преобразуйте выражение (x + 8)2 в многочлен.

Решение:
(x + 8)2 = x2 + 2 × x × 8 + 82 = x2 + 16x + 64

Задание 3. Преобразуйте выражение (2×2 + 3×3)2 в многочлен.

Решение:
(2×2 + 3×3)2 = (2×2)2 + 2 × 2×2 × 3×3 + (3×3)2 = 4×4 + 12×5 + 9×6

Задание 4. Преобразуйте выражение (5a + 5)2 в многочлен.

Решение:
(5a + 5)2 = (5a)2 + 2 × 5a × 5 + 52 = 25a2 + 50a + 25

Задание 5. Преобразуйте выражение (9 − x)2 в многочлен.

Решение:
(9 − x)2 = 92 − 2 × 9 × x + x2 = 81 − 18x + x2

Задание 6. Преобразуйте выражение (x − 25)2 в многочлен.

Решение:
(x − 25)2 = x2 − 2 × x × 25 + 252 = x2 − 50x + 625

Задание 7. Преобразуйте выражение (3×2 − y3)2 в многочлен.

Решение:
(3×2 − y3)2 = (3×2)2 − 2 × 3×2 × y3 + ( y3)2 = 9×4 − 6x2y3 + y6

Задание 8. Выполните умножение (x − y)(x + y)

Решение:
(x − y)(x + y) = x2 − y2

Задание 9. Выполните умножение (2x − y)(2x + y)

Решение:
(2x − y)(2x + y) = (2x)2 − y2 = 4×2 − y2

Задание 10. Выполните умножение (7 + 3y)(3y − 7)

Решение:
(7 + 3y)(3y − 7) = (3y)2 − 72 = 9y2 − 49

Задание 11. Выполните умножение (x2 − 5)(x2 + 5)

Решение:
(x2 − 5)(x2 + 5) = (x2)2 − 52 = x4 − 25

Задание 12. Выполните умножение (a3 − b2)(a3 + b2)

Решение:
(a3 − b2)(a3 + b2) = (a3)2 − (b2)2 = a6 − b4

Задание 13. Выполните умножение (5a2 + 2b3)(5a2 − 2b3)

Решение:
(5a2 + 2b3)(5a2 − 2b3) = (5a2)2 − (2b3)2 = 25a4 − 4b6

Задание 14. Выполните умножение (9x − y2)(y2 + 9x)

Решение:
(9x − y2)(y2 + 9x) = (9x)2 − (y2)2 = 81×2 − y4

Задание 15. Выполните умножение (2 − x)(4 + 2x + x2)

Решение:
(2 − x)(4 + 2x + x2) = 23 − x3 = 8 − x3

Задание 16. Выполните умножение (3 − 2)(9 + 6 + 4)

Решение:
(3 − 2)(9 + 6 + 4) = 33 − 23 = 27 − 8 = 19

Задание 17. Выполните умножение (4x + 1)(16×2 − 4x + 1)

Решение:
(4x + 1)(16×2 − 4x + 1) = (4x)3 + 13 = 64×3 + 1

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Формы профиля

Изделия могут отличаться еще и формой профиля, определяющим его назначение. Сечения изделия бывает:

• кольцевым;

• серповидным;

• смешанным.

Арматура кольцевидной формы профиля используется для обеспечения качественного сцепления между собой готовых железобетонных конструкций, серповидного – применяется для бетонных конструкций. За счет нее увеличивается прочность бетона при работе на растяжение.

Материал смешанного профиля – это новинка металлопроката. Начал он выпускаться совсем недавно. В настоящее время такой профиль применяется только при возведении плотин и мостов. Его закладывают в железобетонные элементы, что бы повысить прочность конструкции.